Contestant(alt). Rank 459. Rating +64.
A. Sasha and Array Coloring
题意
给定一个序列,将其用任意数量的颜色染色,染色后,统计每一种颜色中最大值和最小值的差,取和后得到结果。输出最大的结果。
思路
很显然,直接排个序,然后不断将两头的元素取出作为一种颜色做差即可。
时间复杂度:\(O(n \log n)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define ppii pair<int, pii>
#define pci pair<char, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(),x.end()
const int N = 2e5 + 10, mod = 998244353, inf = 0x3f3f3f3f3f3f3f3f;
void solve() {
int n;
cin >> n;
vector<int> a(n);
for(int i=0;i<n;i++){
cin >> a[i];
}
sort(all(a));
int ans = 0;
for(int i=0;i<n/2;i++) ans += a[n - i - 1] - a[i];
cout << ans << '\n';
}
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while(t --) solve();
}签到
B. Long Long
题意
给定一个序列,定义操作为选择一段区间,并将这个区间内的所有元素取相反数。输出任意次操作后的序列的最大总和,并输出要达到这样的总和需要至少操作几次。
思路
首先,总和最大肯定是绝对值之和。
如果我们选择两个负数作为区间的两端,那么如果中间有正数,我们就需要多次操作,显然我们还不如直接选择这两个负数单独操作。
因而,我们考虑对连续的负数区间进行一次操作,最后的操作数就是满足条件的区间数。
值得一提的是,负数区间可以包含 \(0\),但我们不统计只包含 \(0\) 不包含负数的区间。
时间复杂度:\(O(n)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define ppii pair<int, pii>
#define pci pair<char, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(),x.end()
const int N = 2e5 + 10, mod = 998244353, inf = 0x3f3f3f3f3f3f3f3f;
void solve() {
int n;
cin >> n;
vector<int> a(n + 1);
int sum = 0, cnt = 0;
bool f = false;
for(int i=1;i<=n;i++){
cin >> a[i];
sum += abs(a[i]);
if(a[i] < 0) f = true;
if(a[i] > 0 && f) f = false, cnt ++;
}
if(f) cnt ++;
cout << sum << ' ' << cnt << '\n';
}
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while(t --) solve();
}也是签到
C. Sum in Binary Tree
题意
对于一个满二叉树,定义标号方式为按行从左到右编号。
因而我们可以得到前 \(15\) 个元素构造得到的二叉树如下:
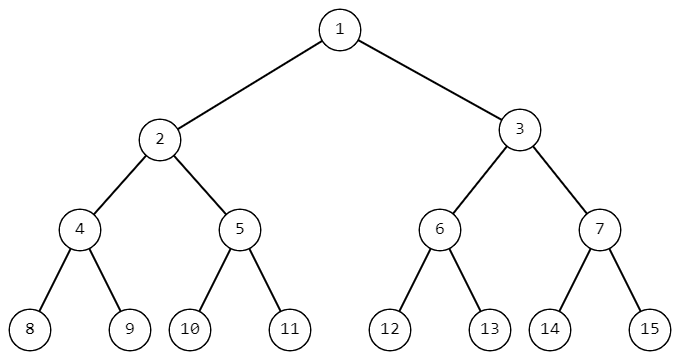
现在,给定一个点 \(x\),输出从根节点 \(1\) 到 \(x\) 的路径上的节点标号之和。
思路
因为每一层的节点数量都是 \(2\) 的次方,不难发现我们只需不断将 \(x\) 除以 \(2\) 向下取整,直到 \(x\) 变为 \(0\),并统计操作前的所有 \(x\) 的总和,即可得到答案。
时间复杂度:\(O(log_2 n)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define ppii pair<int, pii>
#define pci pair<char, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(),x.end()
const int N = 2e5 + 10, mod = 998244353, inf = 0x3f3f3f3f3f3f3f3f;
void solve() {
int n;
cin >> n;
int ans = 0;
while (n > 0) {
ans += n;
n /= 2;
}
cout << ans << '\n';
}
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while(t --) solve();
}差点没看懂题
D. Apple Tree
题意
给定一棵树,对于 \(q\) 次询问,每次给出两个节点 \(x, y\),输出二元组 \((a, b)\) 的个数,满足 \(a\) 在 \(x\) 或 \(x\) 的子树中,\(b\) 在 \(y\) 或 \(y\) 的子树中。
思路
我们直接 \(\mathtt{dfs}\) + \(dp\) 即可,\(dp[i]\) 表示第 \(i\) 个节点子树的节点数量加上自己。
那么 \(dp[x] \times dp[y]\) 即为答案。
时间复杂度:\(O(m + q)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define ppii pair<int, pii>
#define pci pair<char, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(),x.end()
const int N = 2e5 + 10, mod = 998244353, inf = 0x3f3f3f3f3f3f3f3f;
void solve() {
int n;
cin >> n;
vector<int> dp(n + 1);
vector<vector<int>> e(n + 1);
for(int i=1;i<n;i++){
int u, v;
cin >> u >> v;
e[u].pb(v), e[v].pb(u);
}
auto dfs = [&](auto dfs, int s, int f) -> void{
if(s != 1 && e[s].size() == 1) dp[s] ++;
for(auto v : e[s]){
if(v == f) continue;
dfs(dfs, v, s);
dp[s] += dp[v];
}
};
int q;
cin >> q;
dfs(dfs, 1, 0);
while(q --){
int a, b;
cin >> a >> b;
cout << dp[a] * dp[b] << '\n';
}
}
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while(t --) solve();
}这题面...在考验我的耐心
E. Tracking Segments
题意
对于一个长为 \(n\) 的序列,一开始序列内元素都是 \(0\)。
给定 \(m\) 个区间,以及 \(q\) 次操作。每次操作给定一个下标 \(x\),并将 \(x\) 位置的元素改为 \(1\)。
输出在哪次操作后,存在至少一个区间内的元素中 \(1\) 的个数严格大于 \(0\)。
思路
显然,如果操作次数越少,满足条件的区间就更少,反之更多。
因此,此处存在单调性。
我们考虑二分答案,并对操作进行判断。
判断过程可以使用前缀和,在用差分构建完后,我们只需遍历区间,找出是否有一个区间满足条件即可。
时间复杂度:\(O(n \log n)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define ppii pair<int, pii>
#define pci pair<char, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(),x.end()
const int N = 2e5 + 10, mod = 998244353, inf = 0x3f3f3f3f3f3f3f3f;
void solve() {
int n, m;
cin >> n >> m;
vector<pii> a(m + 1);
for(int i=0;i<m;i++) cin >> a[i].fs >> a[i].sc;
int q;
cin >> q;
vector<int> qu(q);
for(int i=0;i<q;i++) cin >> qu[i];
auto check = [&](int x){
vector<int> sum(n + 1);
for(int i=0;i<x;i++) sum[qu[i]] = 1;
for(int i=1;i<=n;i++) sum[i] += sum[i - 1];
for(int i=0;i<m;i++){
auto [l, r] = a[i];
if(sum[r] - sum[l - 1] > r - l + 1 - (sum[r] - sum[l - 1])) return true;
}
return false;
};
int l = 1, r = q, mid;
int ans = -1;
while(l <= r){
mid = (l + r) >> 1;
if(check(mid)) r = mid - 1, ans = mid;
else l = mid + 1;
}
cout << ans << '\n';
}
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while(t --) solve();
}太久不做二分答案了,一时没想到
F1. Omsk Metro (simple version)
题意
对于一个无向图,定义点权均为 \(1\) 或 \(-1\)。
初始状态下只有一个根节点,点权为 \(1\),定义询问如下:
\(+\ V_i\ X_i\),在 \(V_i\) 节点上插入一个点权为 \(X_i\) 的点,新的点的标号为当前最大标号 \(+ 1\);
\(?\ U_i\ V_i\ K_i\),输出从 \(U_i\) 到 \(V_i\) 这条路径上是否有一段子路径(连续子序列)满足点权和为 \(K_i\)。
给定 \(q\) 个询问,执行对应操作。
在 \(simple\) 版本中,第二种询问的 \(U_i\) 恒为 \(1\),即根节点。
思路
首先,既然一个端点固定是根节点,我们就可以将这张图抽象为一颗树,从根节点到所有叶节点的路径都可以单独提出来作为一个序列来看待,那么,我们直接考虑某一条路径:
不难发现,当我们添加节点的时候,因为点权只有 \(1, -1\),那么最后 \(k\) 的取值一定是一段连续的区间,并且随着我们添加节点,区间在不断扩张。
换句话说,我们可以维护 \(k\) 取值的左右端点,在加入节点时扩展左右端点,此时我们不难发现左右端点的取得具有递推性。
因而,我们考虑在图上 \(dp\)。
我们定义 \(dp\_mn[p][v]\) 为 从 \(1\) 节点到 \(v\) 节点中是否以 \(v\) 作为区间端点 的左端点,\(dp\_mx\) 同理。
那么,我们可以得到下面的状态转移方程:
\(dp\_mx[0][x] = \max(dp\_mx[0][v], dp\_mx[1][v])\\dp\_mx[1][x] = \max(dp\_mx[1][v]+x, x)\)
\(dp\_mn\) 同理,将 \(\max\) 改成 \(\min\) 即可。
时间复杂度:\(O(n)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define ppii pair<int, pii>
#define pci pair<char, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(),x.end()
const int N = 2e5 + 10, mod = 998244353, inf = 0x3f3f3f3f3f3f3f3f;
void solve() {
int q;
cin >> q;
vector<vector<int>> dp_mx(2, vector<int>(q + 2)),
dp_mn(2, vector<int>(q + 2));
dp_mx[1][1] = dp_mn[1][1] = 1;
dp_mn[0][1] = dp_mx[0][1] = 0;
int mx = 1;
while (q--) {
char op;
cin >> op;
if (op == '+') {
int v, x;
cin >> v >> x;
mx ++;
dp_mx[0][mx] = max(dp_mx[0][v], dp_mx[1][v]);
dp_mx[1][mx] = max(dp_mx[1][v] + x, x);
dp_mn[0][mx] = min(dp_mn[0][v], dp_mn[1][v]);
dp_mn[1][mx] = min(dp_mn[1][v] + x, x);
} else {
int u, v, k;
cin >> u >> v >> k;
if (min(dp_mn[0][v], dp_mn[1][v]) <= k
&& max(dp_mx[0][v], dp_mx[1][v]) >= k)
cout << "YES\n";
else cout << "NO\n";
}
}
}
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while(t --) solve();
}抽象之,做的时候一直想着前缀
F2. Omsk Metro (hard version)
待补充,区别是不一定有一个端点是根节点