Practice.
A. Select Three Sticks
题意
给定 \(n\) 根火柴,定义操作为选定一根火柴,并将其长度加 \(1\) 或减 \(1\)。输出最小的操作数,使得所有火柴中有至少三根火柴的长度相等。
思路
很显然,我们只需将火柴按长短升序排序,然后枚举所有相邻的三元组,找出 将 左右两个元素 加减 到 与中间的元素相同 所需的操作数 的最小值 即可。
时间复杂度:\(O(n \log n)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fs first
#define sc second
const int N = 110, inf = 0x3f3f3f3f3f3f3f3f;
void solve(){
int n;
cin >> n;
vector<int> a(n);
for(int i=0;i<n;i++) cin >> a[i];
sort(a.begin(), a.end());
int ans = inf;
for(int i=0;i<n-2;i++){
ans = min(ans, a[i + 2] - a[i]);
}
cout << ans << '\n';
}
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while(t --) solve();
}就乱猜(
B. Bright, Nice, Brilliant
题意
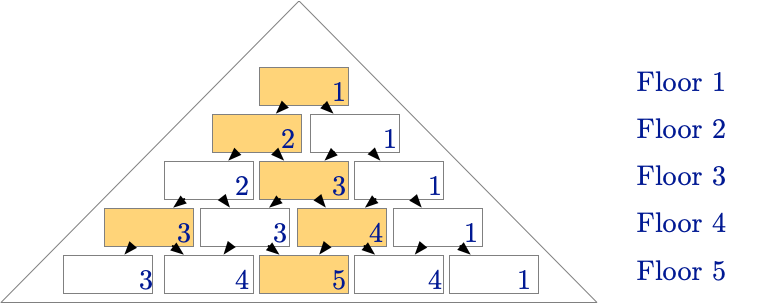
给定一个 \(n\) 层的金字塔,第 \(i\) 层有 \(i\) 个房间,每个房间可选择是否点亮,点亮可以将该房间以及其 "子树" 的亮度 \(+1\),如下图:
现在,给定金字塔的层数,输出每个房间是否点亮 \((0/1)\),满足所有房间的亮度相同,且点亮的房间数最大。
思路
显然,我们只能按照下面的方法构造:
\(\ \ \ \ \ \ \ \ 1 \\\ \ \ \ \ \ 1\ \ 1\\ \ \ \ \ 1\ \ 0\ \ 1\\\ \ 1\ \ 0\ \ 0\ \ 1\\ 1 \ \ 0\ ...\ 0\ \ 1\)
否则,中间一定会越来越大。
时间复杂度:\(O(n ^ 2)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fs first
#define sc second
const int N = 110, inf = 0x3f3f3f3f3f3f3f3f;
void solve(){
int n;
cin >> n;
cout << 1 << '\n';
for(int i=2;i<=n;i++){
cout << 1 << ' ';
for(int j=0;j<i-2;j++) cout << 0 << ' ';
cout << 1 << '\n';
}
}
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while(t --) solve();
}别问,问就是猜的
C. Removing Smallest Multiples
题意
给定一个长为 \(n\) 的二进制字符串,代表 \(1 - n\) 中的数字是否在序列中。
对于上述字符串描述的序列,定义操作为选择任意一个 \(k \in [1, n]\),将序列中最小的 \(k\) 的倍数删去,代价为 \(k\)。
输出最小的代价和,将 \(n\) 的排列变为该序列。
思路
显然,一个数被他的最小因数删去是代价最小的,但我们也需要保证 比这个数更小的 它的最小因数的倍数 不在序列中,否则我们会优先删去不可以删去的元素。
所以我们可以从小到大枚举 \(k\)。
对于 \(k\),我们枚举 \(k\) 的所有倍数(包括 \(k\) 本身),并将所有倍数的答案和 \(k\) 取最小值。
在枚举倍数的时候,只要这个倍数在字符串中对应位置为 \(1\),那么我们直接结束枚举,因为我们会删除不必要的元素。
最后,我们直接遍历每个数的代价,求和即可。
时间复杂度:\(O(n \log n)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fs first
#define sc second
const int N = 110, inf = 0x3f3f3f3f3f3f3f3f;
void solve() {
int n;
cin >> n;
string s;
cin >> s;
s = " " + s;
vector<int> ans(n + 1, inf);
int res = 0;
for (int i = 1; i <= n; i++) {
for (int j = i; j <= n; j += i) {
if (s[j] == '1') break;
ans[j] = min(ans[j], i);
}
if (ans[i] != inf) res += ans[i];
}
cout << res << '\n';
}
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while(t --) solve();
}挺快的(
D. Slime Escape
题意
给定 \(n\) 个史莱姆,每个史莱姆有对应的血量,血量可以为负。给定目标史莱姆的位置,满足该史莱姆的血量为正。
规定目标史莱姆可以向左右任意移动,但每次只能移动一格,移动到对应格时会吸收该格的史莱姆(不可以重复吸收),吸收后,目标史莱姆的血量将会加上被吸收的史莱姆的血量(吸收负血量史莱姆将会扣除目标史莱姆的血量)。
输出目标史莱姆是否可以以非负的血量来到左端点或右端点。
思路
我们用双指针 \(l, r\) 表征目标史莱姆拓展的区域,显然当 \(l \leq 0\) 或 \(r \geq n\) 时到达了端点。
那么,我们只需模拟史莱姆的移动即可,我们默认向左走,那么如果不可以向左,我们就尝试向右,不能移动就结束。
时间复杂度:\(O(n)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fs first
#define sc second
const int N = 110, inf = 0x3f3f3f3f3f3f3f3f;
void solve() {
int n, k;
cin >> n >> k;
vector<int> a(n + 2), pre(n + 2);
for(int i=1;i<=n;i++) cin >> a[i], pre[i] = pre[i - 1] + a[i];
int l = k - 1, r = k;
int l_pre = pre[l], r_pre = pre[r];
while(l > 0 && r < n){
if(r_pre - pre[l - 1] >= 0) l_pre = min(l_pre, pre[-- l]);
else if(pre[r + 1] - l_pre >= 0) r_pre = max(r_pre, pre[++ r]);
else break;
}
cout << (l > 0 && r < n ? "NO\n" : "YES\n");
}
signed main(){
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while(t --) solve();
}这就A了?