Contestant'. Rank 472. Rating +58 (+408 -350).这场没WA!!! 开心捏
A. Love Story
题意
对于字符串 "codeforces",给定一个与其长度相等的字符串,按位遍历,输出不同位置的个数。
思路
如题,暴力即可。
时间复杂度:\(O(n)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(), x.end()
#define r_all(x) x.rbegin(), x.rend()
const int inf = 0x3f3f3f3f3f3f3f3f;
void solve(){
string s;
cin >> s;
string cf = "codeforces";
int cnt = 0;
for(int i=0;i<s.size();i++){
if(s[i] != cf[i]) cnt ++;
}
cout << cnt << '\n';
}
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while (t --) solve();
}签到签到
B. Blank Space
题意
给定一个 \(01\) 序列,输出连续 \(0\) 长度的最大值。
思路
不妨绕一下,在开头和末尾加上 \(1\),那么我们只需枚举 \(1\),求出间距的最大值 \(-1\) 即可。
时间复杂度:\(O(n)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(), x.end()
#define r_all(x) x.rbegin(), x.rend()
const int inf = 0x3f3f3f3f3f3f3f3f;
void solve(){
int n;
cin >> n;
vector<int> a(n + 2, 1);
for(int i=1;i<=n;i++) cin >> a[i];
int pre = 0, cnt = 0;
for(int i=1;i<=n+1;i++){
if(a[i] == 1){
cnt = max(cnt, i - pre - 1);
pre = i;
}
}
cout << cnt << '\n';
}
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while (t --) solve();
}枚举 \(0\) 怕写错就换了个思路
C. Mr. Perfectly Fine
题意
现在有两个知识点需要修学。
给定 \(n\) 本书,每本书具有时间代价 \(m_i\),以及对于两个知识点是否可以修学到。后者用两位二进制表示,如 \(01\) 表示可以花费 \(m_i\) 的时间来修学到知识点 \(2\)。同一个时刻只能学习一本书。
输出两个知识点均修学所需的最小时间代价。
思路
我们遍历输入,分别找出 \(10, 01, 11\) 对应的时间代价最小值 \(l, r, lr\)。
那么,\(ans = \min(l + r, lr)\)。
为了方便判断能否均修学,我们可以初始化三个变量的值为 \(inf\),然后只需判断最后的 \(ans\) 是否大于等于 \(inf\) 即可。
时间复杂度:\(O(n)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(), x.end()
#define r_all(x) x.rbegin(), x.rend()
const int inf = 0x3f3f3f3f3f3f3f3f;
void solve(){
int n;
cin >> n;
int l = inf, r = inf, lr = inf;
for(int i=0;i<n;i++){
int m;
string s;
cin >> m >> s;
if(s == "10") l = min(l, m);
else if(s == "01") r = min(r, m);
else if(s == "11") lr = min(lr, m);
}
int ans = min(l + r, lr);
if(ans >= inf) cout << -1 << '\n';
else cout << ans << '\n';
}
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while (t --) solve();
}题目有点绕
D. Gold Rush
题意
给定一堆金子,金子数量为 \(n\),定义一次操作为选定某一堆金子并将其恰好划分为 \(x, 2x\)。输出任意次操作后能否出现一堆金子的个数为 \(m\)。
思路
首先,既然能划分,那么这个数一定是 \(3\) 的倍数。
不难发现,最后的若干堆金子一定是 \(n\) 整除 \(k\) 个 \(3\) 后,再乘上 \(p, p \in [0, k]\) 个 \(2\) 后得到的。
那么,我们只需暴力,在每次整除 \(3\) 后都枚举一遍 \(p\),判断是否可以相等即可。
时间复杂度:不会算
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(), x.end()
#define r_all(x) x.rbegin(), x.rend()
const int inf = 0x3f3f3f3f3f3f3f3f;
int two[64];
void init(){
two[0] = 1;
for(int i=1;i<64;i++){
two[i] = two[i - 1] * 2;
}
}
void solve(){
int n, m;
cin >> n >> m;
if(n == m){
cout << "YES\n";
return;
}
int k = 0;
while(n % 3 == 0){
k ++, n /= 3;
if(m % n != 0) continue;
for(int i=0;i<=k;i++){
if(n * two[i] == m){
cout << "YES\n";
return;
}
}
}
cout << "NO\n";
}
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
init();
int t = 1;
cin >> t;
while (t --) solve();
}卡了一会儿
E. The Lakes
题意
给定一个 \(n \times m\) 的矩阵,元素为非负数。
对于当前位置,定义移动的限制为:
只能向上下左右移动一位;
不能移动到 \(0\);
不能越界;
不能移动到之前经过的点
定义一条路径为任选一个不为 \(0\) 的点,并进行符合要求的若干次移动后的最大路径,这条路径的贡献为所有在该路径上的点的值的和。
输出最大的路径贡献。
思路
一道很裸的搜索题。
就这样,手搓一下 \(dfs\) 的板子即可。
至于起点的话,按顺序枚举,跳过已经遍历过的点和为 \(0\) 的点即可。
时间复杂度:\(O(nm)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(), x.end()
#define r_all(x) x.rbegin(), x.rend()
const int inf = 0x3f3f3f3f3f3f3f3f;
int two[64];
void init(){
two[0] = 1;
for(int i=1;i<64;i++){
two[i] = two[i - 1] * 2;
}
}
void solve(){
int n, m;
cin >> n >> m;
if(n == m){
cout << "YES\n";
return;
}
int k = 0;
while(n % 3 == 0){
k ++, n /= 3;
if(m % n != 0) continue;
for(int i=0;i<=k;i++){
if(n * two[i] == m){
cout << "YES\n";
return;
}
}
}
cout << "NO\n";
}
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
init();
int t = 1;
cin >> t;
while (t --) solve();
}无脑搓板子(
F. Forever Winter
题意
定义雪花图如下:
无向图;
选定一个点为雪花的中心点;
中心点和 \(x\) 个点连接;
对于这 \(x\) 个点,均有 其他 \(y\) 个点和它连接
现在,给定一个雪花图,输出上述定义中的 \(x, y\)。
保证 \(\min(x, y) \geq 2\)
思路
我们遍历所有的叶节点,也就是度为 \(1\) 的点,这些点个数总和就是 \(xy\)。
对于一个叶节点,他一定只有一个点和其相连,也就是定义中那 \(x\) 个点的其中一个。
那么,我们只需统计所有叶节点所连接的不同点的个数,个数即为 \(x\)。
由上,可相除求得 \(y\)。
可以证明,对于题目所给限制,上述算法一定成立。
时间复杂度:\(O(n + m)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(), x.end()
#define r_all(x) x.rbegin(), x.rend()
const int inf = 0x3f3f3f3f3f3f3f3f;
void solve(){
int n, m;
cin >> n >> m;
vector<vector<int>> e(n + 1);
vector<int> in(n + 1);
for(int i=0;i<m;i++){
int u, v;
cin >> u >> v;
e[u].pb(v);
e[v].pb(u);
in[u] ++, in[v] ++;
}
vector<bool> st(n + 1);
int x = 0, y = 0;
for(int i=1;i<=n;i++){
if(in[i] == 1) {
y ++;
if(!st[e[i][0]]) x ++, st[e[i][0]] = true;
}
}
cout << x << ' ' << y / x << '\n';
}
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while (t --) solve();
}抽象
G. Hits Different
题意
将 \(2023\) 个格子按照下图的规律放置成一个金字塔:
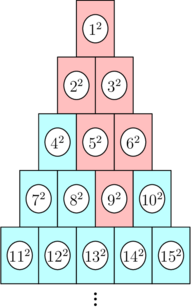
定义一个点的所有顶部的点为 当前层标记的所有点 与上一层相邻的点 并依次递归到最顶部为止 后被标记的所有点。
如上图,对于 \(9\),除了它本身,其余被标红的点就是它所有顶部的点。
给定 \(n\),输出其本身以及其所有顶部点的值之和。
题目明示开 \(long\ long\)。
思路
首先,我们不难发现,我们要求和的点就是一个倒三角内的所有点。
这个倒三角很有趣,我们以例图为例,来看看规律如何:
从 \(9\) 开始,向右上角枚举,最后枚举到了 \(6\),也就是第三行的末尾;
对于 \(9, 6\),向左上角求和,恰好都有 \(3\) 个数,\(3\) 就是 \(6\) 的行数;
向左上角枚举,扣除 当前行数,向右上角枚举,扣除 (当前行数 \(-1\))
通过归纳猜想我们可以得出,我们循环从 \(n\) 开始,依次扣除 (当前行数 \(-1\)),直到遍历到第 \(x\) 行的末尾,并记录我们遍历了 \(cnt\) 个数。
那么,最后的答案就是 \(cnt\) 个前缀和长度为 \(x\) 的和。
此处为按照 \(1 \rightarrow 3 \rightarrow 6\) 为一行,\(1 \rightarrow 2 \rightarrow 4\) 为一列的方式计算每行的前缀和。
那么,前缀和我们完全可以预处理,枚举即可。
时间复杂度:不大
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(), x.end()
#define r_all(x) x.rbegin(), x.rend()
const int N = 3e3, M = 4e6, inf = 0x3f3f3f3f3f3f3f3f;
int sum[N][N];
int line[M];
bool ed[M];
void init(){
int start = 1;
for(int i=1;i<=2e3;i++){
int cur = start;
for(int j=1;j<=2e3-i+1;j++){
sum[i][j] = sum[i][j - 1] + cur * cur;
cur += i + j;
}
start += i;
}
int now = 0;
for(int i=1;i<=2e3;i++){
for(int j=1;j<=i;j++){
now ++;
line[now] = i;
}
ed[now] = true;
}
}
void solve(){
int n;
cin >> n;
int tmp = n, cnt = 1;
while(!ed[tmp]){
tmp -= line[tmp] - 1;
cnt ++;
}
int to = line[tmp];
int ans = 0;
for(int i=1;i<=cnt;i++) ans += sum[i][to];
cout << ans << '\n';
}
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
init();
int t = 1;
cin >> t;
while (t --) solve();
}纯纯找规律(
H. Don't Blame Me
题意
给定序列 \(a\) 以及整数 \(k\),输出子序列的个数,满足序列中所有数按位与以后得到的数的二进制中有 \(k\) 个 \(1\)。
思路
根据题目所给数据范围,可以推测这道题需要状压枚举。
考虑到非连续子序列,我们可以推测这道题需要 \(dp\)。
下面给出状压 \(dp\) 的解法:
首先,对于当前位置,它既可以作为某些子序列的一部分,也可以不作为任何子序列的一部分,当然也可以作为新序列的开头。
因此,我们定义 \(dp[i][j]\) 为前 \(i\) 个数的所有子序列在 \(i\) 位为值 \(j\) 的个数,进行分讨:
作为某些子序列的一部分,我们枚举 \(msk \in [1, 63]\),并将 \(dp[i][msk \& a[i]]\) 加上 \(dp[i - 1][msk]\);
不作为任何子序列的一部分,那么跳过这个元素,\(dp[i][msk]\) 加上 \(dp[i - 1][msk]\);
作为新序列的开头,\(dp[i][a[i]]\) 加上 \(1\)。
最后,我们枚举所有二进制下 \(1\) 的个数为 \(k\) 的数 \(msk\),并统计 \(dp[n][msk]\) 的总和即可。
时间复杂度:\(O(2^6n)\)
对应AC代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pii pair<int, int>
#define fs first
#define sc second
#define pb emplace_back
#define all(x) x.begin(), x.end()
#define r_all(x) x.rbegin(), x.rend()
const int N = 3e3, M = 4e6, inf = 0x3f3f3f3f3f3f3f3f, mod = 1e9 + 7;
int set_bit(int x){
int cnt = 0;
while(x > 0){
if(x % 2 == 1) cnt ++;
x /= 2;
}
return cnt;
}
void solve(){
int n, k;
cin >> n >> k;
vector<vector<int>> dp(n + 1, vector<int>(1 << 6, 0));
for(int i=1;i<=n;i++){
int cur;
cin >> cur;
for(int msk = 0; msk < (1 << 6); msk ++){ //状压枚举
dp[i][msk] = (dp[i][msk] + dp[i - 1][msk]) % mod; //作为某些子序列中不出现的元素
dp[i][msk & cur] = (dp[i][msk & cur] + dp[i - 1][msk]) % mod; //作为某些子序列的一部分
}
dp[i][cur] = (dp[i][cur] + 1) % mod; //新开一个子序列
}
int ans = 0;
for(int msk = 0; msk < (1 << 6); msk ++){
if(set_bit(msk) == k) ans = (ans + dp[n][msk]) % mod;
}
cout << ans << '\n';
}
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int t = 1;
cin >> t;
while (t --) solve();
}你还真别说,我赛时确实想到了状压 \(dp\),不会写罢了(x